Answer:
0.1667 = 16.67% probability that she/he has diabetes
Explanation:
Conditional Probability
We use the conditional probability formula to solve this question. It is

In which
P(B|A) is the probability of event B happening, given that A happened.
 is the probability of both A and B happening.
is the probability of both A and B happening.
P(A) is the probability of A happening.
In this question:
Event A: Living below the poverty level.
Event B: Having diabetes.
30% of the elderly people are living below poverty level.
This means that
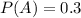
5% of the elderly population falls into both of these categories.
This means that
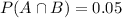
If a randomly selected elderly person is living below the poverty level, what is the probability that she/he has diabetes
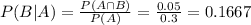
0.1667 = 16.67% probability that she/he has diabetes