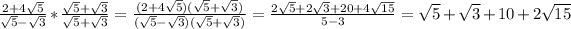Question

I-

please. help.
I have a test soon and I don’t know anything please.

Answer 1

The answer is √5+√3+10+2√15

Answer 2

Answer:
`√(5) + √(3) + 10 + 2√(15)`

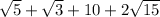
Explanation:

`(2+4√(5) )/(√(5)-√(3) )`

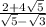
You need to multiply by the conjugate

To find the conjugate, first remember:

(a+b)(a-b) = a^2 - b^2 (if a and b are sqrts, this will eliminate the square roots, rationalizing the denominator)

You have √5 - √3 as the denominator

You should multiply by √5 + √3

(This will eliminate the sqrts)

Remember to multiply both the numerator and denominator

`(2+4√(5) )/(√(5)-√(3) ) = (2+4√(5) )/(√(5)-√(3) ) * (√(5)+√(3) )/(√(5)+√(3))`

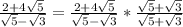
Now simplify

`(2+4√(5) )/(√(5)-√(3) ) * (√(5)+√(3) )/(√(5)+√(3)) = ((2+4√(5))(√(5)+√(3)))/((√(5)-√(3))(√(5)+√(3))) = (2√(5)+2√(3)+20+4√(15))/(5-3) = √(5) + √(3) + 10 + 2√(15)`