Question

Find the length of UC

Answer 1

18

Explanation:

One way to solve this would be to just solve for random lengths, left to right, until we come to find UC.

We know JK = JH + HM + MK = 82 and JH = 22, so

82 = 22 + HM + MK

subtract 22 from both sides to isolate the unknowns

60 = HM + MK = HK

96 = HK + KU - HU

We know HK = 60

96 = 60 + KU

subtract 60 from both sides to isolate the unknown

We know KU = 36

105 = KN = KU + UC + CN

We know KU = 36 and CN = 51

105 = 36 + 51 + UC

105 = 87 + UC

subtract 87 from both sides to isolate the unknown

18 = UC

UC is what we're looking for, so the problem is solved

Answer 2

The length of UC is 18 units.

To find the length of UC, we need to use the given information and equations involving other lengths. Let's break down the solution step by step:

Step 1:

Find the length of HK by first establishing the equation for JK:

`JK = JH + HM + MK.`

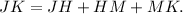
Given that
`JH = 22`

`82 = 22 + HM + MK`

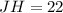
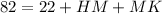
Subtract 22 from both sides to isolate the unknowns:

`60 = HM + MK = HK.`

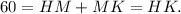
Step 2:

Incorporate HK into the equation involving KU:

`96 = HK + KU - HU.`

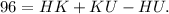
Substituting
`HK = 60`

`96 = 60 + KU.`

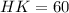
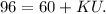
Subtract 60 from both sides to isolate the unknown:

`36 = KU.`

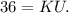
Step 3:

Utilize KU and solve for UC in the final equation:

`105 = KU + UC + CN.`

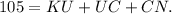
Given that
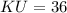`KU = 36` , and
`CN=51`

`105 = 36 + 51 + UC.`

`105 = 87 + UC.`

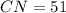
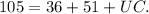
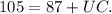
Subtract 87 from both sides to isolate the unknown:

`18 = UC`

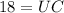
Therefor, the length of UC is 18 units.