Answer:
There is a sufficient evidence that the coefficient b1 is not zero
There is a sufficient evidence that the coefficient b2 is not zero
Explanation:
Given



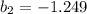

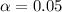
Claim: Coefficient is zero
The null and alternate hypotheses are:
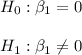
The test is two tailed because the alternate hypothesis contains
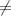
Calculate the rejection region
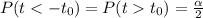
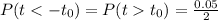

Calculate the degrees of freedom
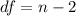
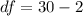
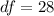
On the student's T distribution table, the t value at 28 and column with
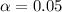 (two tailed) is:
(two tailed) is:
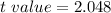
The rejection value will contain all value lesser than -2.048 and all values greater than 2.048.
So: We reject
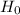 when
when
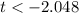 and
and
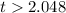
Testing the first independent variable
Calculate test statistic
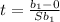
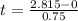
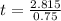

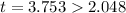
This implies that, we reject
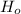 and accept
and accept
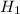
There is a sufficient evidence that the coefficient b2 is not zero
Testing the second independent variable
Calculate test statistic
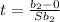
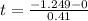


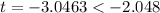
This implies that, we reject
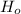 and accept
and accept
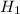
There is a sufficient evidence that the coefficient b2 is not zero