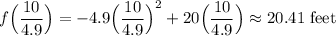Question

A model rocket is launched directly upward at a speed of 20 meters per second from the ground. The function f(t)=−4.9t2+20t, models the relationship between the height of the rocket and the time after launch, t, in seconds. When, in seconds after launch, will the rocket reach its highest point? Round to two decimal places.

Answer 1

The rocket will reach its highest point about 2.04 seconds.

Explanation:

The function:

`f(t)=-4.9t^2+20t`

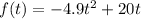
Models the relationship between the height of the rocket and the time after launch t in seconds.

Since this is a quadratic function, the rocket will reach its highest point at its vertex. The vertex of a quadratic is given by:

`\displaystyle \Big(-(b)/(2a), f\Big(-(b)/(2a)\Big)\Big)`

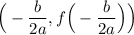
In this case, a = -4.9, b = 20, and c = 0. Thus:

`\displaystyle t=(-(20))/(2(-4.9))=(10)/(4.9)\approx 2.04`

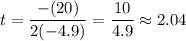
The rocket reaches its maximum height after 10/4.9 or about 2.04 seconds.

Further Notes:

Then the maximum height of the rocket will be f(10/4.9):

`\displaystyle f\Big((10)/(4.9)\Big)=-4.9\Big((10)/(4.9)\Big)^2+20\Big((10)/(4.9)\Big)\approx20.41\text{ feet}`