Question

An elementary school is offering 3 language classes: one in Spanish, one inFrench, and one in German. The classes are open to any of the 100 students inthe school. There are 28 students in the Spanish class, 26 in the French class,and 16 in the German class. There are 12 students that are in both Spanish andFrench, 4 that are in both Spanish and German, and 6 that are in both Frenchand German. In addition, there are 2 students taking all 3 classes.(a) If a student is chosen randomly, what is the probability that he or she isnot in any of the language classes

Answer 1

0.5 = 50% probability that he or she is not in any of the language classes.

Explanation:

We treat the number of students in each class as Venn sets.

I am going to say that:

Set A: Spanish class

Set B: French class

Set C: German class

We start building these sets from the intersection of the three.

In addition, there are 2 students taking all 3 classes.

This means that:

`(A \cap B \cap C) = 2`

6 that are in both French and German

This means that:

`(B \cap C) + (A \cap B \cap C) = 6`

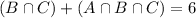
So

`(B \cap C) = 4`

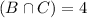
4 French and German, but not Spanish.

4 that are in both Spanish and German

This means that:

`(A \cap C) + (A \cap B \cap C) = 4`

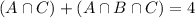
So

`(A \cap C) = 2`

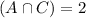
2 Spanish and German, but not French

12 students that are in both Spanish and French

This means that:

`(A \cap B) + (A \cap B \cap C) = 12`

So

`(A \cap B) = 10`

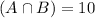
10 Spanish and French, but not German

16 in the German class.

This means that:

`(C - B - A) + (A \cap C) + (B \cap C) + (A \cap B \cap C) = 16`

`(C - B - A) + 2 + 4 + 2 = 16`

`(C - B - A) = 8`

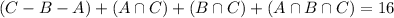
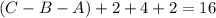
8 in only German.

26 in the French class

`(B - C - A) + (A \cap B) + (B \cap C) + (A \cap B \cap C) = 26`

`(B - C - A) + 10 + 4 + 2 = 26`

`(B - C - A) = 10`

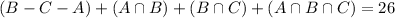
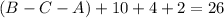
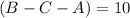
10 only French

28 students in the Spanish class

`(A - B - C) + (A \cap B) + (A \cap C) + (A \cap B \cap C) = 16`

`(A - B - C) + 10 + 2 + 2 = 28`

`(A - B - C) = 14`

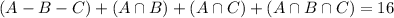
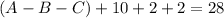
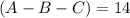
14 only Spanish

At least one of them:

The sum of all the above values. So

`(A \cup B \cup B) = 14 + 10 + 8 + 10 + 2 + 4 + 2 = 50`

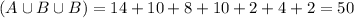
None of them:

100 total students, so:

`100 - (A \cup B \cup B) = 100 - 50 = 50`

(a) If a student is chosen randomly, what is the probability that he or she is not in any of the language classes?

50 out of 100. So

50/100 = 0.5 = 50% probability that he or she is not in any of the language classes.