Answer:
There is not enough statistical evidence to conclude that the cumulative incidence of prostrate cancer among 50-year old men differs from that of 70-year old men
Explanation:
The population 10 year cumulative incidence of prostrate cancer among 70 year old men, p = 0.06
The number of 50 year old men in the sample, n = 260 men
The number of the sampled men that developed prostrate cancer = 13 men
The significance level, α = 0.05
Let the null hypothesis, H₀:
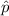 = p
= p
The alternative hypothesis, Hₐ:
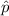 ≠ p
≠ p
The standard score,
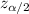 = 1.96
= 1.96
The test statistic, 'z', is given as follows;
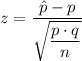
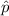 = 13/260 = 0.05
= 13/260 = 0.05
q = 1 - p = 1 - 0.06 = 0.94
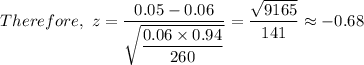
From the z-table, we find the p-value as follows;
P(z ≈ -0.68) = 0.24825
Therefore, given that the p-value, 0.24825 is larger than the significance level, α/2 = 0.025, we fail to reject the null hypothesis, and therefore, there is not enough statistical evidence to conclude that the cumulative incidence of prostrate cancer among 50-year old men differs from that of 70-year old men