Answer:
Option B, False
Explanation:
Step 1: Get the surface area formulas for both shapes
Surface Area Formula for Cone:
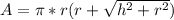
Surface Area Formula for Cylinder:
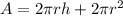
Step 2: Plug in the values and solve
Cone:
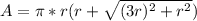
Cone:
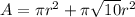
Cylinder:

Cylinder:
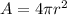
Step 3: Compare
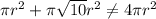
They are not equal, therefore the answer is False.
Answer: Option B, False