Explanation:
There are 5 types of Inequality sign :
1. = read '' equals to ''
2. > read '' greater than ''
3. < read '' less than ''
4. ≥ read '' greater than or equals to ''
5. ≤ read '' less than or equals to ''
Example -
1. 2 = 3 ( 2 is equals to 3 )
2. 3 > 2 ( 3 is greater than 2 )
3. 2< 4 ( 2 is less than 4 )
4. 3 ≥ 2 ( 3 is greater than or equals to 2)
5. 2 ≤ 4 ( 2 is less than or equals to 4 )
One - step inequality :
Addition and Subtraction Properties of Inequality -
If a > b, then a + c > b + c
If a > b, then a − c > b − c
Multiplication and Division Properties of Inequality -
If a > b, then ac > bc, if c > 0
If a > b, then ac < bc, if c < 0
If a > b, then
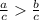, if c > 0
If a > b, then
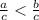,, if c < 0
- The inequality x > y can also be written as y < x. The sides of any inequality can be switched as long as the inequality symbol between them is also reversed(or flip ).
- Solving inequalities is same as solving equations, except you have to reverse( or flip ) the inequality symbols when you multiply or divide both sides of an inequality by a negative number.