Answer:
a)
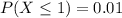

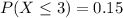

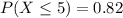
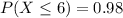
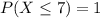
b)
4.61
c) 1.1579
d) 5 is the third quartile of this distribution.
Explanation:
We are given the following discrete distribution:
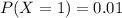




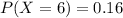

a. Find the cdf of X.
Probability of X being less of equal to x. Than


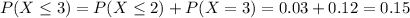
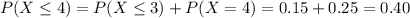
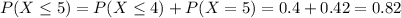

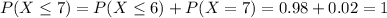
b. Find the expected number of courses a student is taking this semester.
Multiplication of every outcome by its probability.
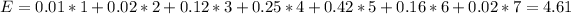
c. Find the variance of X.
Multiplication of the squared subtraction of each value and the mean, multiplied by its probability. So
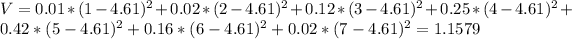
d. Find the third quartile of this distribution.
100*(3/4) = 75th percentile
The cdf passes 0.75 when X = 5, so 5 is the third quartile of this distribution.