Answer:
Part A
The thickness of the compacted soil is approximately 4.3467 × 10⁻¹ m
Part B
The weight of water to be added is approximately 19886.
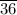 kN, the volume of the water added is approximately 2,027.77 m³
kN, the volume of the water added is approximately 2,027.77 m³
Step-by-step explanation:
The parameters of the soil are;
The volume of sol the excavator excavates,
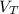 = 10,000 m³
= 10,000 m³
The moist unit weight, W = 17.5 kN/m³
The moisture content = 10%
The area of the project, A = 20,000 m²
The required dry unit weight = 18.3 kN/m³
The required moisture content = 12.5%
Part A
Therefore, we have;
The moist unit weight = Unit weight = (
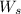 +
+
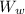 )/
)/
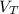
The moisture content, MC = 10% = (
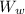 /
/
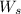 ) × 100
) × 100
∴
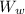 = 0.1·
= 0.1·
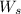
∴ The moist unit weight = 17.5 kN/m³ = (
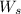 + 0.1·
+ 0.1·
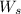 )/(10,000 m³)
)/(10,000 m³)
1.1·
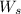 = 10,000 m³ × 17.5 kN/m³ = 175,000 kN
= 10,000 m³ × 17.5 kN/m³ = 175,000 kN
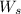 = 175,000 kN/1.1 = 159,090.
= 175,000 kN/1.1 = 159,090.
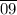 kN
kN
For the required soil, we have;
The required dry unit weight = 18.3 kN/m³ =
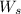 /
/
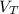 = 159,090.
= 159,090.
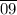 kN/
kN/
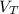
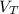 = 159,090.
= 159,090.
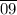 kN/(18.3 kN/m³) ≈ 8,693.4923 m³
kN/(18.3 kN/m³) ≈ 8,693.4923 m³
The total volume of the required soil ≈ 8,693.4923 m³
Volume
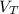 = Area, A × Thickness, d
= Area, A × Thickness, d
∴ d =
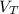 /A
/A
d = 8,693.4923 m³/(20,000 m²) ≈ 4.3467 × 10⁻¹ m
The thickness of the compacted soil ≈ 4.3467 × 10⁻¹ m
Part A
The moisture content, MC = 12.5% = (
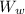 /
/
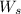 ) × 100
) × 100
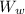 =
=
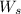 × MC/100 = 159,090.
× MC/100 = 159,090.
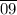 kN × 12.5/100 = 19886.
kN × 12.5/100 = 19886.
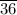 kN
kN
The weight of water to be added,
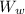 = 19886.
= 19886.
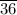 kN
kN
Where the density of water, ρ = 9.807 kN/m³
Therefore, we have;
The volume of water, V =
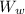 /ρ
/ρ
∴ V = 19886.
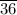 kN/(9.807 kN/m³) ≈ 2027.77 m³
kN/(9.807 kN/m³) ≈ 2027.77 m³
The volume of water, V ≈ 2027.77 m³