Question

Solve for x

Answer choices:
4
5
8
3
2

Answer 1

opposite angles are equal

`\\ \sf\longmapsto 13x+19=84`

`\\ \sf\longmapsto 13x=84-19`

`\\ \sf\longmapsto 13x=65`

`\\ \sf\longmapsto x=(65)/(13)`

`\\ \sf\longmapsto x=5`

Answer 2

`\boxed {\boxed {\sf x=5}}`

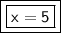
Explanation:

We are asked to solve for x.

We are given a pair of intersecting lines and 2 angles measuring (13x+19)° and 84°. The angles are opposite each other, so they are vertical angles. This means they are congruent or have the same angle measure.

Since the 2 angles are congruent, we can set them equal to each other.

`(13x+19)=84`

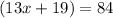
Solve for x by isolating the variable. This is done by performing inverse operations.

19 is being added to 13x. The inverse operation of addition is subtraction. Subtract 19 from both sides of the equation.

`13x+19-19= 84 -19`

`13x= 84 -19`

`13x=65`

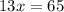
x is being multiplied by 13. The inverse operation of multiplication is division. Divide both sides by 13.

`\frac {13x}{13}= (65)/(13)`

`x= (65)/(13)`

`x= 5`

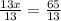
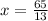
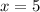
For this pair of vertical angles, x is equal to 5.