Question

The difference between 2 supplementary angles is 121.54. What are the angle measures?

Answer 1

Answer: 150.77 and 29.23

==============================================

Step-by-step explanation:

x = larger angle

y = smaller angle

x-y = difference of the angles = 121.54

x-y = 121.54 is one equation

x+y = 180 is the other equation since supplementary angles always add to 180 (they form a straight line).

We have this system we're working with

`\begin{cases}x-y = 121.54\\x+y = 180\end{cases}`

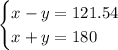
Add the equations straight down.

• x+x = 2x
• -y+y = 0y, the y terms go away
• 121.54+180 = 301.54

We're left with this reduced equation

2x = 301.54

Divide both sides by 2 to isolate x

x = 301.54/2

x = 150.77

Use this to find the value of y

x-y = 121.54

150.77-y = 121.54

-y = 121.54-150.77

-y = -29.23

y = 29.23

Or we could say

x+y = 180

150.77+y = 180

y = 180-150.77

y = 29.23

---------------

Summary:

x = 150.77 and y = 29.23 are the two angles.

I'll let you check the answers.

Answer 2

150.77° and 29.23°

Step-by-step explanation:

Let:

• x = the biggest supplementary angle
• y = the smallest supplementary angle

The sum of the angles is 180*

The difference is 121.54°

The system of equations:

`\left \{ {{x+y=180} \atop {x-y=121.54}} \right.`

Solve:

• Eliminate y by adding vertically

• 
  `\begin{array}{ccc}x+y=180\\+(x-y=121.54)\end/`

• 2x + 0 = 301.54
• 2x = 301.54
• x = 150.77

Now we know what x is, we can plug it into the first equation to solve for y.

• x + y = 180
• 150.77 + y = 180
• y = 29.23

-Chetan K