Answer:
Part A
The work done in pulling the bucket to the top of the well is 1,775 ft.·lb
Part B
By Reimann approximation, the work done is 2,130 ft.·lb
Explanation:
Part A
The parameters of the filled bucket of water being pulled upwards are;
The mass of the bucket = 5 lb
The mass of the rope = Negligible
The mass of water that fills the bucket = 38 lb
The rate at which the bucket is pulled up = 1.5 ft./s
The rate at which the bucket leaks, l = 0.15 lb/s
The height in feet above the bottom of the well = x
Therefore, we have;
Height of the bucket, x = 1.5·t
The weight of the bucket after a given time, t, W = 38 - 0.15·t
The time it takes to pull the bucket to the top of the well, t = d/v = 50/1.5 = 100/3 s. =
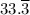 s
s
We have;
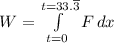
x = 1.5·t, F = Weight of the bucket, W = 38 - 0.15·t
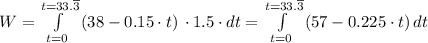
![W = [57\cdot t - 0.225 \cdot t^2]_0^(33.\overline 3)](https://img.qammunity.org/2022/formulas/mathematics/college/yq5iziztji2c0og6vmjg4s7kxpqasb75e5.png)
Therefore, we have;
W = (57 ×
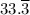 - (0.225/2) ×
- (0.225/2) ×
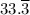 ²) - 0 = 1,775 ft.·lb
²) - 0 = 1,775 ft.·lb
The work done in pulling the bucket to the top of the well, W = 1,775 ft.·lb
Part B
By summing the areas of the rectangular areas on the graph, we have
W = 10 × 38 + 10 × (38 - 0.1×10) + 10 × (38 - 0.1 × 20) + 10 × (38 - 0.1 × 30) + 10 × (38 - 0.1 × 40) + 10 × (38 - 0.1 × 50) = 2,130
Therefore, by left Reimann approximation, the work done, W = 2,130 ft.·lb
(More precisely, we have;
The weight at the bottom, F₁ = 38 lb.
The weight at the top of the well, F₂ = 38 - 0.15 × 100/3 = 33
∴ F₂ = 33 lb.
The average weight,
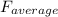 = (F₁ + F₂)/2 = (38 lb. + 33 lb.)/2 = 35.5 lb.
= (F₁ + F₂)/2 = (38 lb. + 33 lb.)/2 = 35.5 lb.
Therefore, the work done,
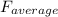 × d = 35.5 lb × 50 ft. = 1,775 ft.lb
× d = 35.5 lb × 50 ft. = 1,775 ft.lb
The work done, W = 1,775 ft.lb)