Question

The two columns below give fertility of eggs of the CP strain of Drosophila melanogaster raised in 100 vials of 10 eggs each (data from R.R. Sokal). Find the expected frequencies, assuming that the mortality for each egg in a vial is independent. Use the observed mean. Calculate the expected variance and compare it with the observed variance. Interpret the results, knowing that the eggs of each vial are siblings and that the different vials contain descendant from different parent pairs. Answer: o2 = 2.417; s2 = 6.628.

Number of Eggs Hatched Number of Vials f Expected Frequency of vials
0 1
1 3
2 8
3 10
4 6
5 15
6 14
7 12
8 13
9 9
10 9

Answer 1

Given the number of the edges are = 11

Therefore we take
`$(1)/(11)=0.091$`

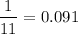
And the number of the vials total is = 100

Thus we can multiply =
`$100 * 0.091 = 9.1$`

From the table provided below, we can obtained :

1. Null hypothesis and alternate hypothesis :

The following null and alternate hypothesis needs to be tested :

`$H_0:p_1=0.091, \ p_2 = 0.091, p_3=0.091, \p_4=0.091, \p_5=0.091, \p_6=0.091, \p_7=0.091,$`
`$p_8=0.091, \ p_9=0.091, \ p_(10)=0.091, \ p_(11)=0.091 $`

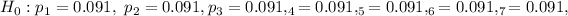
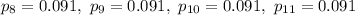
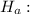`$H_a :$` some of the population differ from the values stated in the null hypothesis. It corresponds the Chi-square test that is for the Goodness of the Fit.

2. Rejection region :

It is given --

significance level, α = 0.05

number of degrees of freedom, df = 11 - 1

= 10

Then the rejection region of this test is :

`$R=\{ x^2:x^2 >18.307\}$`

3. Test statistics

The Chi-Squared statistics is computed as :

`$x^2=\sum_(i=1)^n ((O_i-E_i)^2)/(E_i)$`

`$=7.21+4.089+0.133+0.089+1.056+3.825+2.638+0.924+1.671+0.001+0.001$`

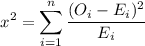
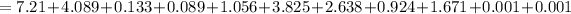
= 21.638

4. Decision about null hypothesis

Since we see that :
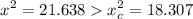`$x^2=21.638>x^2_c = 18.307$`, we can concluded that we can reject the null hypothesis.

5. Conclusion :

It is concluded that the null hypothesis
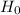`$H_0$` is rejected. So there is enough evidence for us to claim that the population proportions differ from that stated in null hypothesis at α = 0.05 significance level.