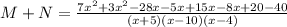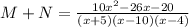Question

Suppose 7x-5 M=- 3 x-8 and NE 2 2 x - 5 x - 50 X - 14 x +40 and you want to add the fractions M and N, in other words you want to compute 7x-5 3 x - 8 2 x - 5 x - 50 x - 14 x + 40 and simplify the result. We know that, before you can add the fractions, you must find a common denominator and rewrite each fraction so it has that common denominator. Once the rewritten fractions have the same denominator, you can add them and simplify the result.

There are four text boxes below. In the first text box, enter a common denominator for the two fractions. In the second text box, rewrite M so that it possesses the common denominator you found. Note that your entry in this text box should equal M, however it should have the common denominator you found. In the third text box, rewrite N so that it possesses the common denominator you found. In the last text box, compute your simplified answer for M N . Make sure that your answer is simplified; the numerator and denominator of your answer for M N should not have common factors. Note that your entry for the common denominator should be a polynomial with integer coefficients. Your other three entries should be fractions that contain polynomials. All of your answers should contain no letters other than the variables that appear in M and N. Do not include an equals sign with any of your answers. All of your expressions should be mathematically correct and not contain non-mathematical symbols. After entering your answers, click the Save Answer button. Your computer will display how your answers were interpreted, and you will have the opportunity to accept these answers or modify them.
Enter a common denominator for M and N here:
Enter M rewritten here:
Enter N rewritten here:
Enter your simplified result here:

Answer 1

`(a)`
`Denominator= (x - 10)(x+5)(x-4)`

`(b)`
`M = ((7x - 5)(x-4))/((x+5)(x - 10)(x-4))`

`(c)`
`N = ((3x - 8)(x + 5))/((x-4)(x-10)(x + 5))`

`(d)`
`M + N = (10x^2-26x -20)/((x+5)(x - 10)(x-4))`

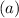
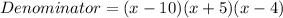
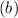
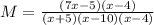
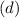
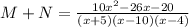
Explanation:

Given

`M = (7x - 5)/(x^2 -5x - 50)`

`N = (3x - 8)/(x^2 -14x+ 40)`

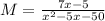
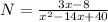
Solving (a): A common denominator of M and N.

To do this, we simply get the LCM of both denominators

`M = x^2 - 5x - 50`

`N = x^2 - 14x + 40`

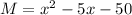
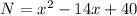
Factorize both:

`M = (x - 10)(x + 5)`

`N = (x- 10)(x - 4)`

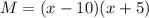
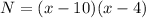
The LCM is

`LCM= (x - 10)(x+5)(x-4)`

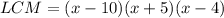
Hence, the common denominator is:

`Denominator= (x - 10)(x+5)(x-4)`

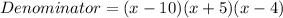
Solving (b): Rewrite M

`M = (7x - 5)/(x^2 -5x - 50)`

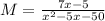
Factor the denominator:

`M = (7x - 5)/((x+5)(x - 10))`

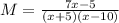
The LCM calculated in (a) above is:

`LCM= (x - 10)(x+5)(x-4)`

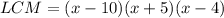
So, we have to multiply the numerator and denominator of M by (x - 4)

The expression becomes:

`M = (7x - 5)/((x+5)(x - 10)) * (x - 4)/(x-4)`

`M = ((7x - 5)(x-4))/((x+5)(x - 10)(x-4))`

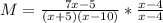
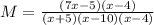
Solving (c): Rewrite N

`N = (3x - 8)/(x^2 -14x+ 40)`

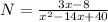
Factor the denominator:

`N = (3x - 8)/((x-4)(x-10))`

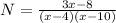
The LCM calculated in (a) above is:

`LCM= (x - 10)(x+5)(x-4)`

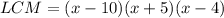
So, we have to multiply the numerator and denominator of N by (x + 5)

The expression becomes:

`N = (3x - 8)/((x-4)(x-10)) * (x + 5)/(x + 5)`

`N = ((3x - 8)(x + 5))/((x-4)(x-10)(x + 5))`

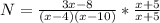
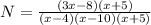
(d) Solve M + N

`M + N = ((7x - 5)(x-4))/((x+5)(x - 10)(x-4)) + ((3x - 8)(x + 5))/((x-4)(x-10)(x + 5))`

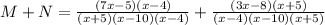
Take LCM

`M + N = ((7x - 5)(x-4) + (3x - 8)(x + 5))/((x+5)(x - 10)(x-4))`

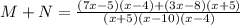
Open brackets

`M + N = (7x^2 - 28x - 5x + 20 + 3x^2 + 15x - 8x - 40)/((x+5)(x - 10)(x-4))`

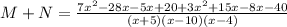
Collect Like Terms

`M + N = (7x^2 + 3x^2- 28x - 5x + 15x - 8x + 20 - 40)/((x+5)(x - 10)(x-4))`

`M + N = (10x^2-26x -20)/((x+5)(x - 10)(x-4))`