Question

Suppose that a uniform rope of length L resting on a frictionless horizontal surface, is accelerated along the direction of its length by means of a force F, pulling it at one end. A mass M is accelerated by the rope. Assuming the mass of the rope to be m and the acceleration is a. Stated in terms of the product ma, what is the tension in the rope at the position 0.3 L from the end where the force F is applied if the mass M is 1.5 times the mass of the rope m?

Answer 1

2.2 ma

Step-by-step explanation:

Given :

Length of the rope = L

Mass of the rope = m

Mass of the object pulled by the rope = M

M = 1.5 m

So, L
`$\rightarrow$` m

For unit length
`$\rightarrow (m)/(L)$`

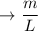
∴ 0.3 L =
`$0.3 \ L \left((m)/(L)\right)$`

= 0.3 m

And for remaining 0.7 L =
`$0.7 \ L \left((m)/(L)\right)$`

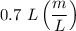
= 0.7 m

By Newtons law of motion,

F - T = ( 0.3 m) a .........(1)

T = ( M + 0.7 m) a

T = ( 1.5 m + 0.7 m) a

T = ( 2.2 m ) a ..............(2)

So from equation (1) and (2), we have

Tension on the rope

T = 2.2 ma