Question

The particle on a ring is a useful model for the motion of electrons around the porphine ring, the conjugated macrocycle that forms the structural basis of the heme group and the chlorophylls. We may treat the group as a circular ring of radius 440 pm, with 22 electrons in the conjugation system moving along the perimeter of the ring. In the ground state of the molecules each state is occupied by two electrons.

A) Calculate the energy and angular momentum of an electron in the highest occupied level.
B) Calculate the frequency of radiation that can induce a transition between the highest occupied and lowest unoccupied levels.

Answer 1

Step-by-step explanation:

The formula for determining the energy of state
`m_l` can be computed by using the formula:

`Em_i = (m_1^2h^2)/(2I)`

Also, the momentum is:

`l_2 = m_i h`

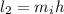
There are 22 electrons with two electrons in each of the lowest II energy levels so that the highest occupied states are
`m_1 = \pm 5`

The moment of inertia of an electron on a ring of radius 440 ppm is:

`I = mR^2 \\ \\ = 9.109 * 10^(31) \ kg (440 * 10^(-12)) ^2 \\ \\ = 1.76 * 10^(-49) \ kgm^2`

`E_(\pm 5 ) = (25h^2)/(2I) \\ \\ = \mathbf{7.89 * 10^(-19) \ J}`

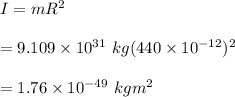
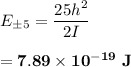
The angular momentum is:

`l_2 = \pm 5h \\ \\ = \pm 5 \tiems ( 1.05457 * 10^(-34) \ Js)`

`= \mathbf{5.275 * 10^(-34) \ Js}`

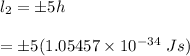
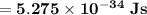
B) Let's recall that:

The lowest occupied energy level is
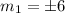`m_1 = \pm 6` which implies that the energy
`E_(\pm 6)= 1.14 * 10^(-18) \ J`

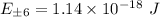
Thus;

`\Delta E = E_(\pm 6) - E_(\pm 5) \\ \\ = 1.14 * 10^(-18 \ J) - 0.79 * 10^(-18) \ J \\ \\ = 0.35 * 10^(-18) \ J \\ \\ 0.35 * 10^(-18) \ J = hv \\ \\ 0.35 * 10^(-18) \ J = h (c)/(\lambda)`

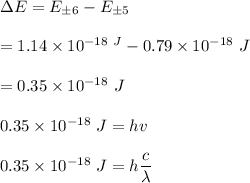
Hence, the radiation which would induce a transition that relates to the wavelength of about 570nm, a wavelength of visible light.