Answer:
The angle of elevation of the rocket is increasing at a rate of 48.780º per second.
Step-by-step explanation:
Geometrically speaking, the distance between the rocket and the observer (
 ), measured in kilometers, can be represented by a right triangle:
), measured in kilometers, can be represented by a right triangle:
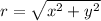 (1)
(1)
Where:
 - Horizontal distance between the rocket and the observer, measured in kilometers.
- Horizontal distance between the rocket and the observer, measured in kilometers.
 - Vertical distance between the rocket and the observer, measured in kilometers.
- Vertical distance between the rocket and the observer, measured in kilometers.
The angle of elevation of the rocket (
 ), measured in sexagesimal degrees, is defined by the following trigonometric relation:
), measured in sexagesimal degrees, is defined by the following trigonometric relation:
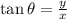 (2)
(2)
If we know that
 , then the expression is:
, then the expression is:
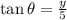
And the rate of change of this angle is determined by derivatives:
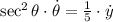
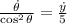
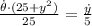

Where:
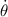 - Rate of change of the angle of elevation, measured in sexagesimal degrees.
- Rate of change of the angle of elevation, measured in sexagesimal degrees.
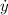 - Vertical speed of the rocket, measured in kilometers per hour.
- Vertical speed of the rocket, measured in kilometers per hour.
If we know that
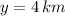 and
and
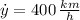 , then the rate of change of the angle of elevation is:
, then the rate of change of the angle of elevation is:
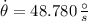
The angle of elevation of the rocket is increasing at a rate of 48.780º per second.