Solution :
Given :
X = homicide rate (homicides per 100,00 population)
n = 12 = metropolitan areas
Area X (homicides per 100,000 population)
Mesa, AZ 4.1
Seattle, WA 3.8
Portland, OR (tie) 3.4
New York, NY(tie) 3.4
Virginia beach, VA 3.3
San Jose, CA 3.1
EI, Paso, TX 2.6
Austin, TX 2.6
San Diago, CA 2.4
Suffolk County 2.2
Montgomery, MD 2.0
Fairfax, VA 1.7
Therefore, the mean of X =
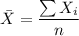
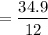
= 2.9
Therefore, the mean of homicide rater in the 12 metropolitan areas is 2.9 homicide per 100,000 population.