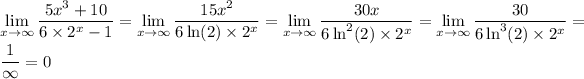For large enough x, exponential functions like 2ˣ will always dominate a polynomial of any degree. This is to say the denominator will always be larger than the numerator (again, for sufficiently large x). So the limit in this case would be 0. (I'll leave a link in comments to a variety of answers regarding this detail.)
But if you've been introduced to L'Hopital's rule: we have