Answer:
0.9225 = 92.25% probability that two or more internship trained candidates are hired.
Explanation:
Candidates are chosen without replacement, which means that we use the hypergeometric distribution to solve this question.
Hypergeometric distribution:
The probability of x sucesses is given by the following formula:
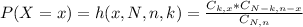
In which:
x is the number of sucesses.
N is the size of the population.
n is the size of the sample.
k is the total number of desired outcomes.
Combinations formula:
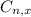 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
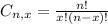
Group of 13 individuals:
This means that
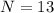
6 candidates are selected:
This means that
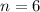
6 in trained internships:
This means that
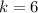
Find the probability that two or more internship trained candidates are hired.
This is:
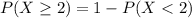
In which
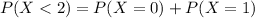
So
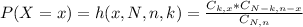
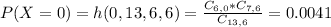
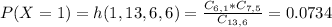
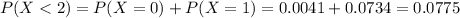
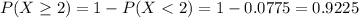
0.9225 = 92.25% probability that two or more internship trained candidates are hired.