Answer:
A)
the minimum stopping distance for which the load will not slide forward relative to the truck is 14 m
B)
data that were not necessary to the solution are;
a) mass of truck and b) mass of load
Step-by-step explanation:
Given that;
mass of load
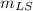 = 10000 kg
= 10000 kg
mass of flat bed
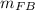 = 20000 kg
= 20000 kg
initial speed of truck
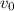 = 12 m/s
= 12 m/s
coefficient of friction between the load sits and flat bed μs = 0.5
A) the minimum stopping distance for which the load will not slide forward relative to the truck.
Now, using the expression
Fs,max = μs
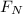 -------------let this be equation 1
-------------let this be equation 1
where
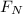 = normal force = mg
= normal force = mg
so
Fs,max = μs mg
ma
 = μs mg
= μs mg
divide through by mass
a
 = μs g ---------- let this be equation 2
= μs g ---------- let this be equation 2
in equation 2, we substitute in our values
a
 = 0.5 × 9.8 m/s²
= 0.5 × 9.8 m/s²
a
 = 4.9 m/s²
= 4.9 m/s²
now, from the third equation of motion
v² = u² + 2as
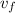 ² =
² =
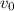 ² + 2aΔx
² + 2aΔx
where
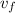 is final velocity ( 0 m/s )
is final velocity ( 0 m/s )
a is acceleration( - 4.9 m/s² )
so we substitute
(0)² = (12 m/s)² + 2(- 4.9 m/s² )Δx
0 = 144 m²/s² - 9.8 m/s²Δx
9.8 m/s²Δx = 144 m²/s²
Δx = 144 m²/s² / 9.8 m/s²
Δx = 14 m
Therefore, the minimum stopping distance for which the load will not slide forward relative to the truck is 14 m
B) data that were not necessary to the solution are;
a) mass of truck and b) mass of load