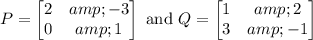Treat the matrices on the right side of each equation like you would a constant.
Let 2X + Y = A and 3X - 4Y = B.
Then you can eliminate Y by taking the sum
4A + B = 4 (2X + Y) + (3X - 4Y) = 11X
==> X = (4A + B)/11
Similarly, you can eliminate X by using
-3A + 2B = -3 (2X + Y) + 2 (3X - 4Y) = -11Y
==> Y = (3A - 2B)/11
It follows that
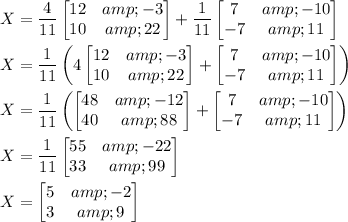
Similarly, you would find
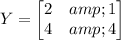
You can solve the second system in the same fashion. You would end up with