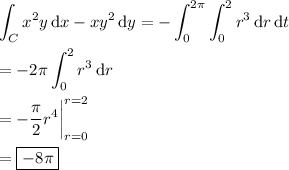Question

b) Use Greens theorem to find∫x^2 ydx-xy^2 dy where ‘C’ is the circle x2 + y2 = 4 going counter clock wise.​

Answer 1

It looks like the integral you want to find is

`\displaystyle \int_C x^2y\,\mathrm dx - xy^2\,\mathrm dy`

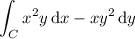
where C is the circle x ² + y ² = 4. By Green's theorem, the line integral is equivalent to a double integral over the disk x ² + y ² ≤ 4, namely

`\displaystyle \iint\limits_(x^2+y^2\le4)(\partial(-xy^2))/(\partial x)-(\partial(x^2y))/(\partial y)\,\mathrm dx\,\mathrm dy = -\iint\limits_(x^2+y^2\le4)(x^2+y^2)\,\mathrm dx\,\mathrm dy`

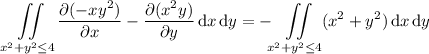
To compute the remaining integral, convert to polar coordinates. We take

x = r cos(t )

y = r sin(t )

x ² + y ² = r ²

dx dy = r dr dt

Then

`\displaystyle \int_C x^2y\,\mathrm dx - xy^2\,\mathrm dy = -\int_0^(2\pi)\int_0^2 r^3\,\mathrm dr\,\mathrm dt \\\\ = -2\pi\int_0^2 r^3\,\mathrm dr \\\\ = -\frac\pi2 r^4\bigg|_(r=0)^(r=2) \\\\ = \boxed{-8\pi}`