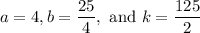Question

Work out the values of a, b and k ? 30 points

Answer 1

`\displaystyle a=4, b= (25)/(4), \text{ and } k = (125)/(2)`

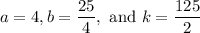
Explanation:

Note that the graph passes through the points: (0, 4), (1, 25), and (1.5, k).

The standard exponential function has the form:

`\displaystyle y = ab^x`

The point (0, 4) tells us that y = 4 when x = 0. Therefore:

`(4) = a(b)^0`

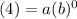
Since anything raised to zero is one:

`a=4`

Hence, our function is now:

`y = 4(b)^x`

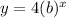
The point (1, 25) tells us that y = 25 when x = 1. By substituting:

`(25) = 4(b)^((1))`

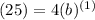
Solve for b:

`\displaystyle b = (25)/(4)`

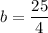
Thus, our completed function is:

`\displaystyle y = 4\left((25)/(4)\right)^x`

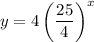
To find k, simply substitute 1.5 for x. This yields:

`\displaystyle y = k = 4\left((25)/(4)\right)^((1.5))`

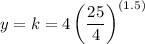
And evaluate. Hence:

`\displaystyle \begin{aligned} k &= 4\left((25)/(4)\right)^(3/2) \\ \\ &= 4\left(\left((25)/(4)\right)^(1/2)\right)^3 \\ \\ &= 4\left((5)/(2)\right)^3 \\ \\ &= 4\left((125)/(8)\right) \\ \\ &= (125)/(2)\end{aligned}`

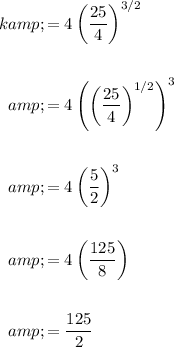
In conclusion:

`\displaystyle a=4, b= (25)/(4), \text{ and } k = (125)/(2)`