Question

The path of an athlete's long jump is modeled by a function h(d)=−14d2+d, where d and h denote the distance and the height in meters respectively. The graph of h(d) is given by

Answer 1

Answer:9ft

Explanation:

Answer 2

Based on the graph of this function, the horizontal length and the maximum height of this jump include;

Horizontal length = 4 meters.

Maximum height = 1 meter.

In Mathematics and Geometry, the graph of a quadratic function would always form a parabolic curve, which ultimately implies that it is a u-shaped curve.

In order to determine the horizontal length (horizontal distance) of the jump, we would have to determine the x-intercept of the graph as follows;

Horizontal length (x-intercept) = 4 meters.

The maximum value of any function is a point on the graph where the function reaches its highest point. In this context, the maximum height of this jump is given by;

Maximum height (peak of graph's h-value) = 1 meter.

Complete Question:

The path of an athlete's long jump is modeled by a function
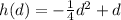`h(d)=- (1)/(4) d^2+d`, where d and h denote the distance and the height in meters respectively. The graph of h(d) is given below. Based on the function's graph, determine the horizontal length and the maximum height of this jump.