Question

drawbridge at the entrance to an ancient castle is raised and lowered by a pair of chains. The figure represents the drawbridge when flat. Find the height of the suspension point of the chain, to the nearest tenth of a meter, and the measures of the acute angles the chain makes with the wall and the drawbridge, to the nearest degree.

Answer 1

4.0 meters, ∠C = 39°, ∠A = 51°

Explanation:

Firstly, our diagram shows us that the given triangle is actually a right triangle. So we can use the Pythagorean Theorem to solve for the height of the chain:

`a^(2) +b^(2) =c^(2)`

`(3.3)^(2) +b^(2) =(5.2)^(2)`

`b^(2) =(5.2)^(2)-(3.3)^(2)`

`b =\sqrt{(5.2)^(2)-(3.3)^(2)}`

`b=4.0187...`

`b=4.0 m`

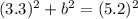
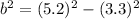
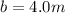
Now, we can use the Law of Cosines to figure out one of the acute angles:

`c^(2) =a^(2) +b^(2) -2ab(cos(C))`

`(3.3)^(2) =(4.0)^(2) +(5.2)^(2) -2(4.0)(5.2)(cos(C))`

`cos(C)=((3.3)^(2)-(4.0)^(2) -(5.2)^(2))/(-2(4.0)(5.2))`

`C=cos^(-1)( ((3.3)^(2)-(4.0)^(2) -(5.2)^(2))/(-2(4.0)(5.2)))`

`C=39.3915...`

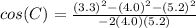
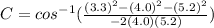
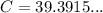
∠C = 39°

And since we know that all angles in a triangle add up to 180°:

∠A + ∠B + ∠C = 180

∠A + 90 + 39 = 180

∠A = 180 - 90 - 39

∠A = 51°

However, you should always review any answers on the Internet and make sure they are correct! Check my work to see if I made any mistakes!