Answer:
4.0 meters, ∠C = 39°, ∠A = 51°
Explanation:
Firstly, our diagram shows us that the given triangle is actually a right triangle. So we can use the Pythagorean Theorem to solve for the height of the chain:
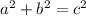
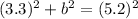
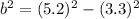
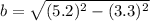
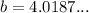
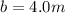
Now, we can use the Law of Cosines to figure out one of the acute angles:

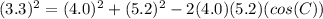
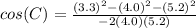
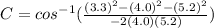
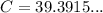
∠C = 39°
And since we know that all angles in a triangle add up to 180°:
∠A + ∠B + ∠C = 180
∠A + 90 + 39 = 180
∠A = 180 - 90 - 39
∠A = 51°
However, you should always review any answers on the Internet and make sure they are correct! Check my work to see if I made any mistakes!