Answer:
Function C is the only one that matches both definitions for the domain and range.
Explanation:
First let's understand what the domain and range definitions mean in plain English.
The following statement means x is defined such that x can be any real number except for 1.
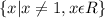
The following statement means y is defined such that y can be any real number except for 3.

So let's see what functions match those definitions. Take a look at the denominator of the functions in question 7, if we plug in x = 1 for any of them, we would be dividing by zero, which we know we can't do since the function would not be defined at that value. Therefore the domain definition is correct for all functions, we cannot use x = 1 for any of them.
Let's move on to the range. Our goal is to find a function where plugging in y = 3 would give us an undefined result. Simply plugin y = 3 into all of the given equations and simplify.
- (A) We find that x = 0, and since the function is defined, we know that the range definition does not match.
- (B) We get the expression -12x + 9 = -3x, where x = 1. Once again the function is defined here, so the range does not match.
- (C) We get 3x - 3 = 3x, which simplifies to -3 = 0. But clearly -3 does not equal 0, which means the function was not defined for y = 3, which means our range definition matches.
- (D) We get -3x = 0, which simplifies to x = 0, which means our function is defined, and our range definition does not match.
Therefore the function C is the only one that matches both definitions for the domain and range.