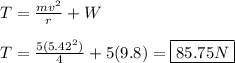Hi there!
We can begin by solving for the pendulum's velocity at the bottom of its trajectory using the work-energy theorem.
Recall:
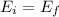
Initially, we just have Potential Energy. At the bottom, there is just Kinetic Energy.
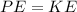
Working equation:
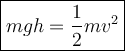
Rearrange to solve for velocity:
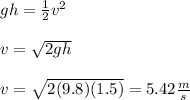
Now, we can do a summation of forces:
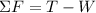
The net force is the centripetal force, so:
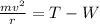
Rearrange to solve for tension: