Answer:
0.6 = 60% probability that a randomly selected application from this distribution took less than 18 minutes.
Explanation:
Uniform probability distribution:
An uniform distribution has two bounds, a and b.
The probability of finding a value of at lower than x is:

The probability of finding a value between c and d is:
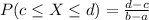
The probability of finding a value above x is:
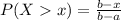
Uniform distribution between 15 and 20 minutes.
This means that
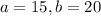
What is the probability that a randomly selected application from this distribution took less than 18 minutes?

0.6 = 60% probability that a randomly selected application from this distribution took less than 18 minutes.