Given:
AD is an angle bisector in triangle ABC.
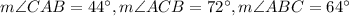 .
.
To find:
The value of
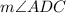 .
.
Solution:
AD is an angle bisector in triangle ABC.
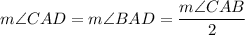
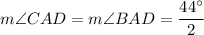
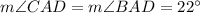
According to the angle sum property, the sum of all interior angles of a triangle is 180 degrees.
Using angle sum property in triangle CAD, we get
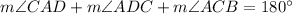
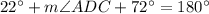
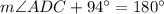
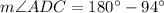
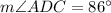
Therefore, the angle of angle ADC is
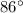 .
.