Question

3. Find any three rational numbers between 1/2 and 3/2​

Answer 1

For example 1/1, 2/3 and 4/3

Explanation:

There is a great way to generate rational numbers between other rational numbers using:

`\textrm{If:~~~~~~} (a)/(b) < (c)/(d)\vspace{7pt}\\\textrm{Then:~} (a)/(b) < (a+c)/(b+d) < (c)/(d)`

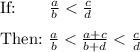
So we know that (1+3)/(2+2) is between 1/2 and 3/2 without checking.

(1+3)/(2+2) = 1/1, so we got our first rational number.

Lets continue by finding numbers between 1/2 and 1/1; and 1/1 and 3/2

(1+1)/(2+1) = 2/3

(1+3)/(1+2) = 4/3

We could also look for a number between 1/2 and 2/3 and find

(1+2)/(2+3) = 3/5

And so on, so forth :)

Answer 2

`(2)/(3) \\ \\ (2)/(2) \\ \\ (4)/(3)`

Explanation:

I hope that is useful for you :)