Question

Which ordered pair would form a proportional relationship with the point graphed below? (60,-20)

Answer 1

Given:

The graphed point is (60,-20).

To find:

The ordered pair that would form a proportional relationship with the given point.

Solution:

If y is proportional to x, then

`y\propto x`

`y=kx`

`(y)/(x)=k`

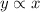
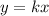
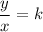
Where, k is the constant of proportionality.

For the given point,

`k=(-20)/(60)`

`k=(-1)/(3)`

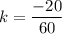
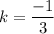
For option (A),

`k=(30)/(-10)`

`k=-3\\eq (-1)/(3)`

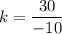
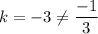
For option (B),

`k=(-15)/(30)`

`k=-(1)/(2)\\eq (-1)/(3)`

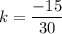
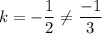
For option (C),

`k=(10)/(-30)`

`k=(-1)/(3)`.

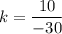
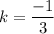The point (-30,10) gives the same value of the constant of proportionality. So, the point (-30,10) forms a proportional relationship with the given point.

Therefore, the correct option is C.