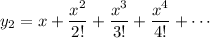Question

Find two power series solutions of the given differential equation about the ordinary point x = 0. Compare the series solutions with the solutions of the differential equation obtained using the method of Section 4.3. Try to explain any differences between the two forms of the solution. y'' − y' = 0 y1 = 1 − x2 2! + x4 4! − x6 6! + and y2 = x − x3 3! + x5 5! − x7 7! + y1 = x and y2 = 1 + x + x2 2! + x3 3! + y1 = 1 + x2 2! + x4 4! + x6 6! + and y2 = x + x3 3! + x5 5! + x7 7! + y1 = 1 + x and y2 = x2 2! + x3 3! + x4 4! + x5 5! + y1 = 1 and y2 = x + x2 2! + x3 3! + x4 4! +

Answer 1

You're looking for a solution in the form

`y(x) = \displaystyle \sum_(n=0)^\infty a_nx^n`

Differentiating, we get

`y'(x) = \displaystyle \sum_(n=0)^\infty na_nx^(n-1) = \sum_(n=1)^\infty na_nx^(n-1) = \sum_(n=0)^\infty (n+1)a_(n+1)x^n`

`y''(x) = \displaystyle \sum_(n=0)^\infty (n+1)na_(n+1)x^(n-1) = \sum_(n=1)^\infty (n+1)na_(n+1)x^(n-1) = \sum_(n=0)^\infty (n+2)(n+1)a_(n+2)x^n`

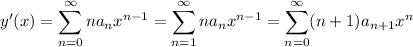
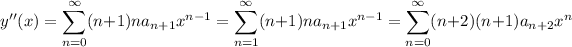
Substitute these for y' and y'' in the differential equation:

`\displaystyle \sum_(n=0)^\infty (n+2)(n+1)a_(n+2)x^n - \sum_(n=0)^\infty (n+1)a_(n+1)x^n = 0`

`\displaystyle \sum_(n=0)^\infty \bigg((n+2)(n+1)a_(n+2)-(n+1)a_(n+1)\bigg)x^n = 0`

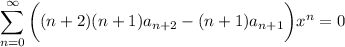
Then the coefficients of y are given by the recurrence

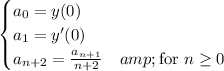
`\begin{cases}a_0=y(0)\\a_1=y'(0)\\a_(n+2)=(a_(n+1))/(n+2)&\text{for }n\ge0\end{cases}`

or

`a_n = \frac{a_(n-1)}n`

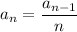
But we cannot assume that
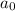`a_0` and
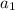`a_1` depend on each other; we can only guarantee that the recurrence holds for n ≥ 1, so that

`a_2=\frac{a_1}2 \\\\ a_3=\frac{a_2}3=(a_1)/(3*2) \\\\ a_4=\frac{a_3}4=(a_1)/(4*3*2) \\\\ \vdots \\\\ a_n=(a_1)/(n!)`

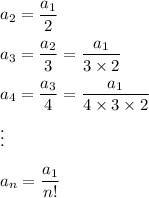
So in the power series solution, we split off the constant term and we're left with

`y(x) = a_0 + a_1 \displaystyle \sum_(n=1)^\infty (x^n)/(n!)`

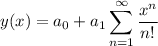
so that the fundamental solutions are

`y_1=1`

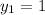
and

`y_2=x+(x^2)/(2!)+(x^3)/(3!)+(x^4)/(4!)+\cdots`