Answer:
Here we only need to analyze the vertical motion of the ball.
First, because the ball is in the air, the only force acting on the ball will be the gravitational force (we are ignoring air resistance), then the acceleration of the ball is equal to the gravitational acceleration, so we have:
a(t) = -32 ft/s^2
where the negative sign is because this acceleration is downwards.
To get the velocity equation, we need to integrate over the time, so we get:
v(t) = (-32 ft/s^2)*t + V0
where V0 is the initial velocity of the ball. In this case, the initial velocity of the ball will be the velocity that the ball had when it was dropped, which should be the same as the velocity of the hot air ballon, so we have:
V0 = 12 ft/s
Then the velocity equation of the ball is:
v(t) = (-32 ft/s^2)*t + 12 ft/s
To get the position equation we integrate again:
p(t) = (1/2)*(-32 ft/s^2)*t^2 + (12 ft/s)*t + H0
Where H0 is the initial height. We know that the ball was released at the height of 1120 ft, then we have:
H0 = 1120 ft.
Then the position equation is:
p(t) = (-16 ft/s^2)*t^2 + (12 ft/s)*t + 1120ft
a) How many seconds after its release will the ball strike the ground?
The ball will strike the ground when its position equation is equal to zero, then we need to solve:
p(t) = 0 ft = (-16 ft/s^2)*t^2 + (12 ft/s)*t + 1120ft
This is just a quadratic equation, the solutions are given by Bhaskara's formula, so the solutions for t are:
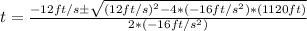
We can simplify that to get:
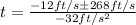
So we have two solutions:
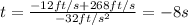
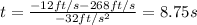
The negative solution does not make sense, then the correct solution is the positive one.
We can conclude that the ball will hit the ground after 8.75 seconds.
b) At what velocity will it hit the ground?
We already know that the ball strikes the ground 8.75 seconds after it is released.
The velocity at it hits the ground is given by the velocity equation evaluated in that time:
v(8.75 s) = (-32 ft/s^2)*8.75s + 12 ft/s = -268 ft/s