Answer:
0.0193 = 1.93% probability that there is equipment damage to the payload of at least one of five independently dropped parachutes.
Explanation:
For each parachute, there are only two possible outcomes. Either there is damage, or there is not. The probability of there being damage on a parachute is independent of any other parachute, which means that the binomial probability distribution is used to solve this question.
To find the probability of damage on a parachute, the normal distribution is used.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
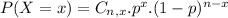
In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
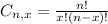
And p is the probability of X happening.
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:
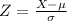
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Probability of a parachute having damage.
The opening altitude actually has a normal distribution with mean value 185 and standard deviation 32 m, which means that
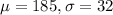
Equipment damage will occur if the parachute opens at an altitude of less than 100 m, which means that the probability of damage is the p-value of Z when X = 100. So
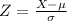
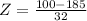

 has a p-value of 0.0039.
has a p-value of 0.0039.
What is the probability that there is equipment damage to the payload of at least one of five independently dropped parachutes?
0.0039 probability of a parachute having damage, which means that
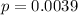
5 parachutes, which means that
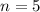
This probability is:
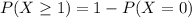
In which
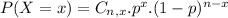
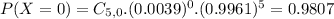
Then
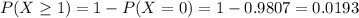
0.0193 = 1.93% probability that there is equipment damage to the payload of at least one of five independently dropped parachutes.