Answer:
The possible coordinates of point A are (-8,-4) or (-8,6)
Explanation:
The distance between two points is given by the formula
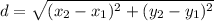
For point A
 ;
;
 and
and
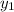 is unknown
is unknown
For point B
 ; (4,1) i.e
; (4,1) i.e
 and
and
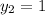
and d = 13
Putting the values into the equation,
![13= \sqrt{[(4-(-8)]^(2) + (1-y_(1))^(2) }\\13= \sqrt{[(4+8)]^(2) + (1-y_(1))^(2) }\\13= \sqrt{12^(2) + (1-y_(1))^(2) }\\13^(2) = 12^(2) + (1-y_(1))^(2) \\169 = 144 +(1-y_(1))^(2)\\169-144 = (1-y_(1))^(2)\\25 = 1 -2y_(1) +y_(1)^(2) \\y_(1)^(2) -2y_(1)+1-25 =0\\y_(1)^(2) -2y_(1)-24 =0\\y_(1)^(2) -6y_(1) + 4y_(1) -24 =0 \\y_(1)(y_(1)-6) +4(y_(1) -6) = 0\\(y_(1)+4)(y_(1)-6) =0\\(y_(1)+4)=0 or (y_(1)-6) =0](https://img.qammunity.org/2022/formulas/mathematics/high-school/sxgelb8zysjqoyo8zi7z50n90h0dvd37nv.png)
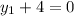 or
or
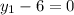
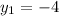 or
or
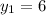
Hence, the possible coordinates of point A are (-8,-4) or (-8,6)