
This theorem states that if a line is drawn parallel || to one side of a triangle ∆ to intersect the other 2 sides in distinct points, the other 2 sides are divided in the same ratio.
From the figure, with the help of this proof, we can see that :-
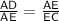
Refer to the attached pictures for the proof & the figure.
_____
Hope it helps.
RainbowSalt2222