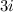Answer:
Real solution,
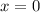
Imaginary solution,
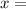 ±
±
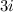
Explanation:
The roots of the equations are the zeros to the equation, in other words, where the equation intersects the x-axis. First, one sets the equation equal to zero, (this is because the roots are the x-intercepts, for these values of x the y-value is zero), then one factor the equation. Finally one uses the zero product property to find the values for which the equation is equal to zero. The zero product property states that any number times zero equals zero.
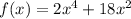
Set equal to zero,
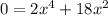
Factor,
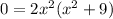
Use the zero product property,
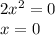
To solve this part of the equation, one must use imaginary numbers. An imaginary number is a way of representing the square root of a negative number, the imaginary unit (
 ) equals;
) equals;
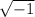 .
.
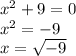
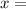 ±
±