Question

The function y=-16r^2+38 represents the height y (in feet) of a water droplet t seconds after falling from an icicle. After how many seconds does the water droplet hit the ground? Round your answer to two decimal places. A second water droplet falls from a height of 41 feet. After how many seconds does that water droplet hit the ground? Round your answer to one decimal place.

Answer 1

The first droplet will hit the ground after about 1.54 seconds.

The second droplet will hit the ground after about 1.6 seconds.

Thus, the first hits the ground first.

Explanation:

We are given the function:

`y=-16r^2 + 38`

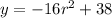
Which represents the height y in feet of a water droplet t seconds after falling from an icicle.

Part A)

We want to find the time it took for the water droplet to hit the ground.

When it hit the ground, its height y above ground will be zero. Therefore, we can let y = 0 and solve for r:

`0=-16r^2+38`

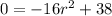
Subtract 38 from both sides:

`-38 = -16 r^2`

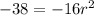
Divide:

`\displaystyle r^2 = (38)/(16) = (19)/(8)`

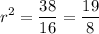
And take the principal square root of both sides:

`\displaystyle r= \sqrt{(19)/(8)} = (√(38))/(4) \approx1.54\text{ seconds}`

So, the first water droplet hits the ground after about 1.54 seconds.

Part B)

We want to determine how long it will take for a water droplet to hit the ground from a height of 41 feet.

From the original equation, if r = 0, then y = 38. So, the initial height was 38 feet.

Then we can modify the function into:

`y= -16r^2 + 41`

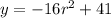
In this case, when r = 0, the starting height y is 41 feet.

Again, let y = 0 and solve for r:

`0 = -16r^2 + 41`

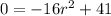
Isolate:

`\displaystyle r^2 = (41)/(16)`

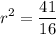
And take the principal square root of both sides:

`\displaystyle r = \sqrt{(41)/(16)} = (√(41))/(4) \approx 1.6\text{ seconds}`

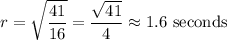
So, the second drop will hit the ground after approximately 1.6 seconds.

And in conclusion, the first drop will hit the ground sooner (as expected).