Question

A random sample of 25 graduates of four-year business colleges by the American Bankers Association revealed a mean amount owed in student loans was $14,381 with a standard deviation of $1,892. Assuming the pop is normally distributed:

a) Compute a 90% confidence interval, as well as the margin of error.
b) Interpret the confidence interval you have computed.

Answer 1

a) The 90% confidence interval for the mean amount owed in student loans of graduates of four-year business colleges is ($13,600, $15,162), having a margin of error of $781.

b) We are 90% sure that the mean amount owed in student loans of graduates of all four-year business colleges is between $13,600 and $15,162.

Explanation:

Question a:

We have the standard deviation for the sample, which means that the t-distribution is used to solve this question.

The first step to solve this problem is finding how many degrees of freedom,which is the sample size subtracted by 1. So

df = 25 - 1 = 24

90% confidence interval

Now, we have to find a value of T, which is found looking at the t table, with 24 degrees of freedom(y-axis) and a confidence level of
`1 - (1 - 0.9)/(2) = 0.95`. So we have T = 2.0639

The margin of error is:

`M = T(s)/(√(n)) = 2.0639(1892)/(√(25)) = 781`

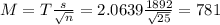
In which s is the standard deviation of the sample and n is the size of the sample.

The lower end of the interval is the sample mean subtracted by M. So it is 14381 - 781 = $13,600

The upper end of the interval is the sample mean added to M. So it is 14381 + 781 = $15,162

The 90% confidence interval for the mean amount owed in student loans of graduates of four-year business colleges is ($13,600, $15,162), having a margin of error of $781.

b) Interpret the confidence interval you have computed.

We are 90% sure that the mean amount owed in student loans of graduates of all four-year business colleges is between $13,600 and $15,162.