Solution :
It is given that the device works satisfactorily if it makes an average of no more than
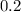 errors per hour.
errors per hour.
The number of errors thus follows the Poisson distribution.
It is given that in
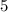 hours test period, the number of the errors follows is
hours test period, the number of the errors follows is
=

= 1 error
Let X = the number of the errors in the
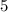 hours
hours
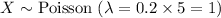
Now that we want to find the
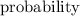 that a
that a
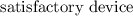 will be misdiagnosed as "
will be misdiagnosed as "
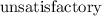 " on the basis of this test. We know that device will be unsatisfactory if it makes more than
" on the basis of this test. We know that device will be unsatisfactory if it makes more than
 error in the test. So we will determine probability that X is greater than
error in the test. So we will determine probability that X is greater than
 to get required answer.
to get required answer.
So the required probability is :
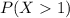

![$=1-[P(X=0)+P(X=1)]$](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/jhrjf2tlybeietzmyo6jb9.png)
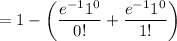
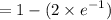

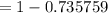
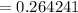
So the
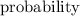 that the
that the
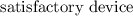 will be misdiagnosed as "
will be misdiagnosed as "
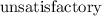 " on the basis of the test whose result is 0.264241
" on the basis of the test whose result is 0.264241