Answer:
x = -6, 10
Explanation:
Hi there!
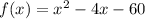
Let f(x) = 0:
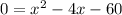
Factor the equation:
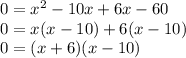
The zero-product property tells us that when two terms are multiplied and they equal zero, one of the terms must be zero.
Therefore, either (x+6) or (x110) is equal to 0:
x+6 = 0 ⇒ x = -6
x-10 = 0 ⇒ x = 10
Therefore, the zeros of f(x) are -6 and 10.
I hope this helps!