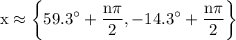Answer:
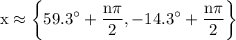
Explanation:
we would like to solve the following trigonometric equation:
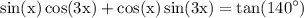
the left hand side can be rewritten using angle sum indentity of sin which is given by:
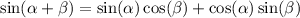
therefore Let
Thus substitute:
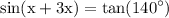
simplify addition:
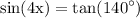
keep in mind that sin(t)=sin(π-t) saying that there're two equation to solve:
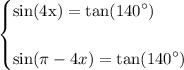
take inverse trig and that yields:
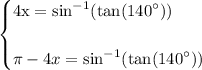
add π to both sides of the second equation and that yields:
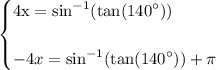
sin function has a period of 2nπ thus add the period:
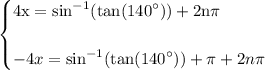
divide I equation by 4 and II by -4 which yields:
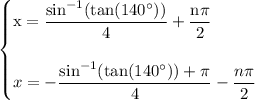
recall that,-½(nπ)=½(nπ) therefore,
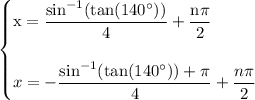
by using a calculator we acquire:
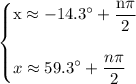
hence,
the general solution for: for the trig equation are