Answer:
The mass of Al is 89.027 kilograms.
The mass of Jo is 104.973 kilograms.
The magnitude of the force of Jo on Al is 596.481 newtons.
Step-by-step explanation:
Given the absence of external forces, this situation can be described will by Principle of Linear Momentum Conservation and Impact Theorem on each skater:
Al:
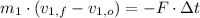 (1)
(1)
Jo:
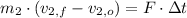 (2)
(2)
Total mass:
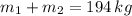
Where:
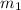 ,
,
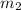 - Masses of the skaters, in kilograms.
- Masses of the skaters, in kilograms.
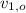 ,
,
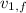 - Initial and final velocities of Al, in meters per second.
- Initial and final velocities of Al, in meters per second.
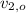 ,
,
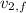 - Initial and final velocities of Jo, in meters per second.
- Initial and final velocities of Jo, in meters per second.
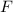 - Impact force between skaters, in newtons.
- Impact force between skaters, in newtons.
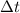 - Impact time, in seconds.
- Impact time, in seconds.
If we know that
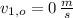 ,
,
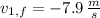 ,
,
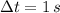 ,
,
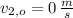 and
and
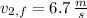 , then the masses of the skaters are, respectively:
, then the masses of the skaters are, respectively:
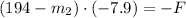 (1b)
(1b)
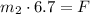 (2b)
(2b)
(2b) in (1b):
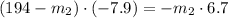
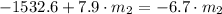
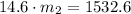
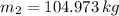
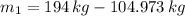
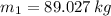
And the magnitude of the force is:
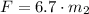
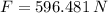
The mass of Al is 89.027 kilograms.
The mass of Jo is 104.973 kilograms.
The magnitude of the force of Jo on Al is 596.481 newtons.