Answer:
a) The proton's speed is 5.75x10⁵ m/s.
b) The kinetic energy of the proton is 1723 eV.
Step-by-step explanation:
a) The proton's speed can be calculated with the Lorentz force equation:
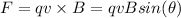 (1)
(1)
Where:
F: is the force = 9.14x10⁻¹⁷ N
q: is the charge of the particle (proton) = 1.602x10⁻¹⁹ C
v: is the proton's speed =?
B: is the magnetic field = 3.28 mT
θ: is the angle between the proton's speed and the magnetic field = 17.6°
By solving equation (1) for v we have:
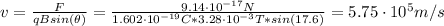
Hence, the proton's speed is 5.75x10⁵ m/s.
b) Its kinetic energy (K) is given by:
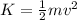
Where:
m: is the mass of the proton = 1.67x10⁻²⁷ kg
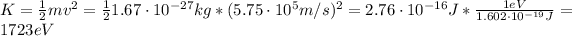
Therefore, the kinetic energy of the proton is 1723 eV.
I hope it helps you!