Answer:
A = 249 x 249 = 62001 square meter.
Side is L = 249 m
Explanation:
Total length of the fence is 996 m.
Let the length is L and the width is W.
Perimeter = 2 (L + W)
996 = 2 (L + W)
498 = L + W
L = 498 - W ...... (1)
Let the area is
A = L W
A = (498 - W) W
A = 498 W - W^2
Differentiate with respect to W.
dA/dW = 498 - 2 W
Put it equal to zero.
498 - 2 W = 0
W = 249 m
Now, L = 498 - 249 = 249 m
Differentiate with respect to W again
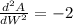
As it is negative so the area is maximum.
The maximum area is
A = 249 x 249 = 62001 square meter.
Side is L = 249 m