Answer:
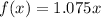
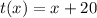
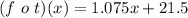
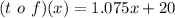
Step-by-step explanation:
Given
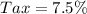
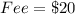 -- delivery
-- delivery
Solving (a): The function for total cost, after tax.
This is calculated as:
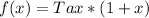
Where:
 total purchase
total purchase
So, we have:
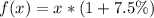
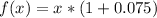
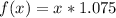
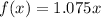
Solving (b): Include the delivery fee
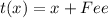
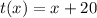
Solving (c): (f o t)(x) and (t o f)(x)

We have:
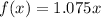
So:
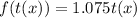
This gives:
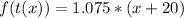
Expand
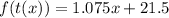
So:
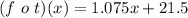
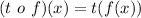
We have:
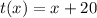
So:
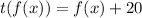
This gives:
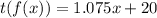
We have:
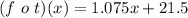 ---- This represents the function to pay tax on the item and on the delivery
---- This represents the function to pay tax on the item and on the delivery
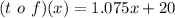 --- This represents the function to pay tax on the item only
--- This represents the function to pay tax on the item only
The x coefficients in both equations are equal.
So, we compare the constants
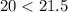 means that (t o f)(x) has a lower cost
means that (t o f)(x) has a lower cost